Kritisk matematisk literacy i ein inquiry-basert kontekst på småskulesteget

Innleiing

Matematikkundervisninga i skulen blir ofte skulda for å vere for dårleg eller for lite relevant. Kunnskapen som elevane tileignar seg gjennom grunnskule og vidaregåande opplæring, har vore utsett for kritikk frå politisk hald (Viseth & Larsen, 2013) og blitt framstilt som for dårleg når elevane kjem til høgare utdanning (Tønnesen, 2016). Det har òg blitt sett på som eit internasjonalt problem at for få elevar er interessert i å studere matematikk (Academia Europaea, 2007). For Noreg har resultata i internasjonale undersøkingar som PISA (OECD, 2017) blitt tolka som skuffande og leidd til store politiske satsingar for å styrke undervisninga, mellom anna ved å satse på vidareutdanning av lærarar gjennom til dømes satsinga Kompetanse for kvalitet. Frå realfagdidaktisk hald har det vore peika på at undervisninga i realfaga bør vere meir elevaktiv og undersøkjande (Maaß & Artigue, 2013). IBL (inquiry-based learning) har blitt halde fram som ein måte å få til meir utforskande og undersøkjande elevaktivitetar i skulen (Rocard, Csermely, Jorde, Lenzen, Walberg-Henriksson & Hemmo, 2007) for der igjennom å auke motivasjon og forståing for realfaga (Bruder & Prescott, 2013). Å tenkje på kva matematikk ein treng for å fungere som samfunnsborgar, er eit sentralt poeng knytt til omgrepet matematisk literacy (t.d. Geiger, Goos & Forgasz, 2015). For å utvikle matematisk literacy blir det peika på at ein må utvikle kritiske evner og ein kritisk tankegang (Goos, Geiger & Dole, 2014). Men kva tyder det å vere kritisk i matematikktimane på skulen, og korleis kan ein leggje til rette for at elevar skal få høve til å vere kritiske? I denne artikkelen undersøkjer vi nettopp dette ved å stille følgjande forskingsspørsmål: Korleis kan arbeid med norske myntar i eit IBL-inspirert klasserom leggje til rette for at elevar på 2. trinn får tenkje kritisk og undersøkje multiple løysingar på matematiske problem?

Teori

Inquiry-basert læring (IBL)

Ved å arbeide meir IBL-orientert vil elevane møte matematikk og naturfag på måtar som er meir lik den måten fagfolk jobbar med desse faga, og elevane blir betre utstyrt til å møte ei usikker framtid der det å stille spørsmål, resonnere, utforske, forklare og utvikle kreative og kritiske haldningar er essensielt (Maaß & Artigue, 2013). Tradisjonelt har realfaga ofte blitt undervist på abstrakt vis der tankegangen har vore at lærdommen elevane tileignar seg i skulen, seinare kan nyttast i ulike kontekstar og yrke. IBL har vist seg å vere ei effektiv tilnærming i rike og røyndomsnære kontekstar og kan ha positiv effekt for elevar som elles presterer svakt (Kogan & Laursen, 2013). Gjennom kontekst-baserte tilnærmingar får elevane innsikt i meiningsfull bruk av realfag, og dette leier til at elevane blir meir motiverte og utviklar gode haldningar til læring, noko som i sin tur påverkar akademiske prestasjonar (Bruder & Prescott, 2013). Ved at elevane blir involvert i autentisk praksis som er undersøkingsbasert og sett inn i rike kontekstar som er knytte til røynda utanfor klasserommet, blir læringsutbyttet ein meir fleksibel og tilpassingsdyktig kompetanse (Gobert & Pallant, 2004). Det finst ikkje nokon universelt godteken definisjon av IBL, men sentrale element som blir trekt fram av fleire, er utvikling av eit spørjande sinn og ei vitskapleg haldning. I denne artikkelen tek vi i bruk modellen utvikla i EU-prosjektet Primas, Promoting Inquiry in Mathematics and Science Education Across Europe (Maaß & Reitz-Koncebovski, 2013). I denne modellen blir aspekt relatert til elevane, lærarane, klasseromskulturen, læringsmiljøet og ønskt utbytte identifisert, sjå figur 1.

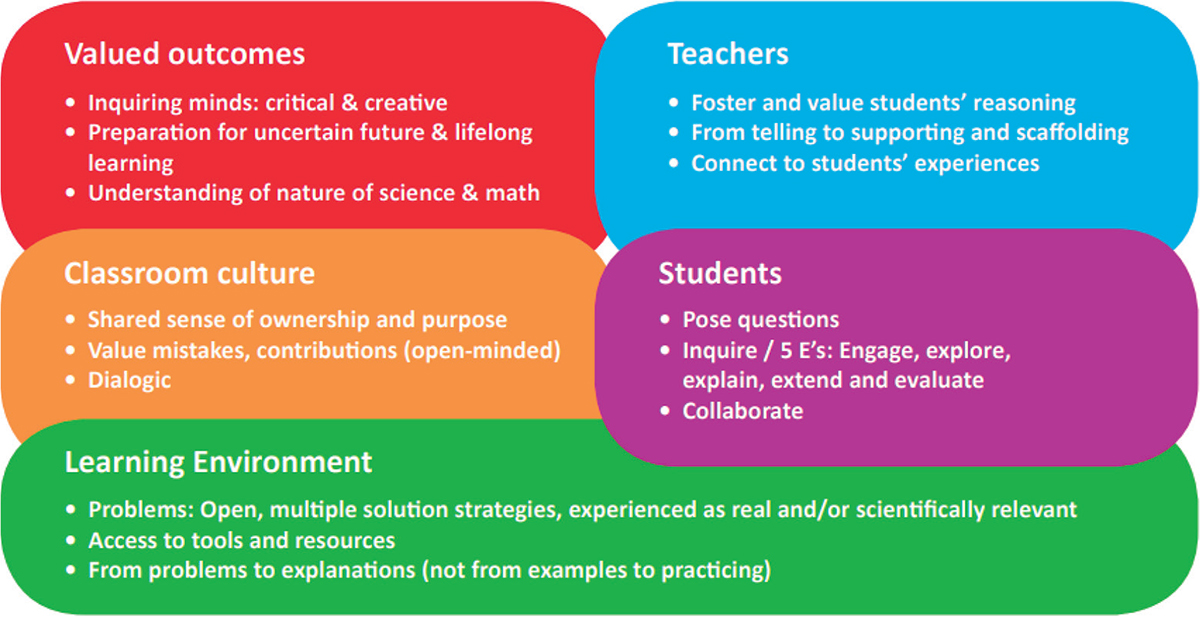
Læringsmiljøet bør vere prega av oppgåver som blir opplevd som relevante og er opne og/eller kan løysast på fleire måtar. Med utgangspunkt i relevante oppgåver skal ein søkje etter forklaringar, i staden for å starte timen med døme på reknemåtar som elevane så skal øve seg på. I eit IBL-prega klasserom er kulturen dialogisk og open på det viset at innspel blir verdsett, inkludert at feil og mistydingar ikkje blir avvist, men blir tekne opp til diskusjon for å lære av dei. Elevane får då ei rolle der det blir verdsett at dei stiller spørsmål, utforskar og samarbeider. Læraren skal oppmuntre elevane til å resonnere, gjere bruk av elevane sine erfaringar og støtte deira arbeid i staden for berre fortelje dei i detalj kva dei skal gjere. Utbyttet av undervisninga bør vere at elevane utviklar seg til å bli tenkjande, kreative og kritiske, noko som tradisjonelt har vore mindre vektlagt i matematikkundervisninga (sjå t.d. Bergem, Nilsen & Scherer, 2016), men som er viktig med tanke på at elevane skal bli utrusta for ei usikker framtid. Då er det òg viktig at dei utviklar forståing for matematikkens natur, mellom anna at matematikk er eit fag som framleis er i utvikling der det er essensielt å stille spørsmål, undersøkje og prøve ut gissingar. Det er viktig å vere klar over at ein ikkje skal forvente å finne att alle dei mogelege kjenneteikna ved IBL i ein kvar klasseromssituasjon. Det ønskte/verdsette utbyttet vil til dømes vere noko ein må arbeide mot på lengre sikt og ikkje forvente å sjå i kvar einskild undervisningsøkt.

Metodologi

Denne artikkelen byggjer på arbeid innanfor eit fleirårig prosjekt knytt til matematisk og naturfagleg literacy i grunnskulen. Didaktikarar frå matematikk- og naturfagseksjonane ved NTNU arbeider saman med to skular i Melhus kommune der vi i fellesskap med lærarar ved skulane planlegg, gjennomfører, observerer, reflekterer over og diskuterer undervisningstimar. Dei to skulane som er med har tidlegare vore med i EU-prosjekt knytt til IBL.

Når ein skal prøve ut nye tilnærmingar til undervisning i klasserommet, er det ein føremon å ikkje stå aleine om utprøvinga. Til dømes peikte Skoumpourdi (2017) på at «it is not easy for teachers to design inquiry-based activities and implement them in the classroom» (s. 1906). Difor er det føremålstenleg å nytte modellar der fleire lærarar går saman om å prøve ut nye pedagogiske tilnærmingar. I slike læringsfellesskap er det òg mange som peikar på nytten av å ha med ekspertar utanfrå, som til dømes didaktikarar frå universitetet. Lesson studies, eller leksjonsstudiar, er ein integrert del av kvardagen for lærarar i Aust-Asia, og har vekt mykje åtgaum i den vestlege verda etter at denne typen læringsfellesskap blei ålment kjent i samband med videostudiar frå japanske klasserom gjennom TIMSS og PISA. Leksjonsstudiar der ein planlegg leksjonar og observerer undervisning i lag i ein syklisk prosess med design og redesign, har blitt haldne fram som ein vellykka type profesjonsutvikling for lærarar (t.d. Yang & Ricks, 2013). I prosjektet vårt startar ein slik syklus ved at lærarane på skulen vel ut eit tema eller eit læringsmål frå læreplanen. Didaktikarane frå universitetet og lærargruppa møtest så for å utvikle ein detaljert plan for ei undervisningsøkt. Ein av lærarane på skulen gjennomfører undervisninga medan resten av lærarane og didaktikarane observerer. Under observasjonen blir det nytta observasjonsskjema som er utarbeidd som ein del av førebuinga til økta. Økta blir teke opp med video-opptakar, samt at læraren har ein lydopptakar på seg gjennom heile økta, og to eller tre lydopptakarar blir òg spreidd i klasserommet ved elevbord. Etter undervisningsøkta møtest didaktikarane og lærarane for å reflektere over gjennomføringa og redesigne opplegget ut frå dei erfaringane som er hausta. Ein av lærarane, som kan vere den same eller ein annan enn den som gjennomførte den første økta, underviser så det redesigna opplegget i ei ny gruppe. Prosedyrane med observasjon og video- og lydopptak er den same. Etter denne økta møtest gruppa på nytt for ny refleksjon, noko som kan munne ut i ein ny redesign. I tillegg til dei data som blir samla inn i samband med leksjonsstudiane, blir lærarar og elevar intervjua ved slutten av skuleåret.

I denne artikkelen ser vi på ei undervisningsøkt i matematikk som blei gjennomført i to elevgrupper i ein lesson study syklus. Elevane var i byrjinga av det andre skuleåret. Det tyder at elevane var 6 eller 7 år gamle då øktene blei gjennomført. I elevgruppa for den første gjennomføringa var det 16 elevar medan det var 14 elevar i den andre gruppa. Det var den same læraren som underviste båe gruppene. Dette er ein av dei to lærarane som underviser i desse to gruppene til dagleg. Læraren hadde fireårig allmennlærarutdanning og ni års erfaring som lærar i barneskulen.

Det matematiske temaet i øktene var addisjon med naturlege tal opp til tjue. Temaet blei introdusert i ein kontekst som involverte norske myntar opp til 20 kroner, altså myntar med verdiane 1 kr, 5 kr, 10 kr og 20 kr. Ved å knyte det reint matematiske temaet, addisjon, til norske myntar får ein ei tilknyting til den «verkelege» verda. For ungar er leik ein stor og viktig del av den verkelege verda, slik at bruk av pengar både kan knytast til leikeverda dei kjenner gjennom å til dømes leike butikk, og samstundes til vaksenverda der kjennskap til pengar er ein naudsynt del av å kunne fungere i samfunnet. Oppgåvene blei presentert som små «mysterium» som elevane skulle vere med å finne ut av, og hadde difor karakter av å vere ekte problem og ikkje reine matematikkoppgåver. Oppgåvene er attgjevne i tabell 1.

Ein viktig del av oppgåvedesignet var å få fram at i matematiske problemstillingar kan talet på løysingar variere: eintydig løysing, fleire løysingar, uendeleg mange løysingar eller inga løysing. I tillegg kjem at det som regel er mange vegar fram mot eit svar, og i desse oppgåvene stod elevane fritt med tanke på korleis dei ville angripe dei, utan tanke på at dei skulle følgje ein fastlagd algoritme. For elevane var det dessutan sett opp som eit eksplisitt mål at dei skulle samarbeide, noko som mellom anna innebar at dei skulle snakke saman medan dei arbeidde med oppgåvene. Kvar time var delt i tre delar: 1) innleiing rundt tavla i lyttekroken; 2) gruppearbeid der elevane jobba to og to. Oppgåvene var trykt på laminerte A5-ark og blei delt ut til elevane etter kvart som dei bad om ny oppgåve; 3) avsluttande plenum der elevane presenterte resultata sine og desse blei diskutert. I arbeidet med oppgåvene hadde elevane tilgang til leikepengar med verdiane 1, 5, 10 og 20, tal-liner, A3-ark, blyantar og teiknestiftar i ulike fargar.

Datamaterialet vi har brukt for denne artikkelen er video- og lydopptak i klasserommet frå dei to øktene og transkripsjonane av desse, kopiar av A3-arka som elevane skreiv på under arbeidet, samt utfylte observasjonsskjemaa frå øktene. Lærarane og dei føresette til elevane har gjeve informert samtykke til deltaking i prosjektet, inkludert at det blir teke lyd- og video-opptak i klasserommet. Elevane sjølve er òg informerte munnleg om kva det handlar om. Prosjektet er meldt inn og godkjend av NSD.

Dataanalysen blei gjennomført ved at vi (dei to forfattarane) først satt saman og såg på video-opptaka frå dei to undervisningsøktene. Dersom noko var uklart i videoen, konsulterte vi dei tilhøyrande lydopptaka eller kopiane av elevarka. Saman med undervisningsplanen og observasjonsskjemaa gav dette oss eit overblikk over øktene. Etterpå sat vi kvar for oss og analyserte transkripsjonane langs to dimensjonar: 1) Kva kjenneteikn ved IBL slik det er identifisert i figur 1 (Maaß & Reitz-Koncebovski, 2013) kan vi finne att i timen? 2) Kva spor av dei tre måtane å vere kritisk på som Askew (2015) identifiserte, kan vi finne att hos elevane? Vi møttest dernest for å utveksle notat og diskutere funna våre for slik å auke reliabiliteten av analysen. Under dette arbeidet konsulterte vi video- eller lydopptaka eller elevarka dersom det var noko som var uklart.

Resultat

Av dei seks tilgjengelege oppgåvene blei alle elevane ferdige med dei to første, medan berre fire elevpar fekk sett på oppgåve 2b) og 1 par på 2c). I denne artikkelen avgrensar vi oss til å sjå på oppgåvene 1a), 1b), 1c) og 2a).

Elevane byrja med Oppgåve 1a: Jens har fire myntar i lomma si. Til saman er det 17 kr. Kva for myntar har Jens i lomma si? Dette er ei oppgåve med eintydig svar, men vegen fram mot svaret er ikkje gjeven. Nokre elevpar teikna myntar på arket sitt, nokre skreiv opp eit addisjonsstykke med tal (typisk 10 + 5 + 1 + 1). Ei gruppe brukte teljestrekar som dei samla i femmarbuntar før dei skreiv tal i eit addisjonsstykke. Dei fleste gruppene brukte ein kombinasjon av dei ulike representasjonane. Ei gruppe teikna opp ei tikrone, ei femkrone og to kronestykke og skreiv reknestykket 10 + 5 + 2 = 17. Gruppene gjorde seg òg nytte av leikemyntane som var tilgjengelege. Ei gruppe hadde nytta leikepengane til å finne svaret, og følte at læraren avbraut dei i det vidare arbeidet då ho bad dei om å i tillegg skrive og teikne. Dei gav uttrykk for at dei hadde løyst oppgåva allereie før læraren gav ei kort påminning til heile klassen om at dei måtte samarbeide i gruppene og gjere seg nytte av dei tilgjengelege ressursane. Denne plenumspåminninga blei oppfatta som ei forstyrring for dei:

24 Elev 2: Vi er allereie ferdige med desse myntane. Vi klarte å finne ut av det før du byrja med den prate-greia.

27 Lærar: Før eg prata?

28 Elev 2: Og vi …

30 Lærar: Men du, kan de ikkje seie korleis de tenkte, og skrive det her? Teikne myntane, skrive addisjonsstykket? Skriv svaret.

Her ser vi at elevane har ei løysing på oppgåva, men i staden for å be dei forklare korleis dei tenkte då dei brukte leikemyntane, oppmodar læraren dei til å framstille løysinga på papiret. På den måten ber læraren dei reflektere over korleis dei har løyst oppgåva og kva for representasjon dei har nytta seg av. Dei får dimed høve til å vere kritiske innanfor den matematiske modellen, ved å sjå si løysing med dei konkrete leikemyntane opp mot løysingar som inneber skriftleggjering av det same. Å vere kritisk innanfor den matematiske modellen er det første av dei tre punkta som Askew (2015) nemnte som måtar å vere kritisk på.

Oppgåve 1b: Jens har 17 kr i lomma si. Kva for myntar kan det vere? Denne oppgåva har fleire løysingar, men berre endeleg mange så lenge ein held seg til norske myntar.

66 Elev 1: OK. 17 kroner, OK. Ein tiar, pluss fem, pluss to. 15, og to einarar. Sånn. Du kan skrive det.

67 Elev 2: Skal eg skrive det same svaret?

69 Elev 1: Nei, nei, nei, du tek forskjellige måtar.

Dei to elevane oppklarer seg imellom om dei skal skrive det same svaret som i 1a). Elev 1 er klar på at i denne oppgåva kan dei finne fleire svar enn det dei fann i 1a). Elevane held fram med å utforske fleire måtar å få til 17 kroner med bruk av norske myntar, og innser at det finst ein god del måtar. Når læraren kjem til bordet deira, seier dei at dei kan fylle heile arket sitt med løysingar på denne oppgåva:

104 Elev 2: Vi finn på kanskje heile arket berre på b-en

Denne typen oppgåve med mange løysingar er framleis ikkje vanleg i norske klasserom eller i lærebøkene. TIMSS-undersøkingane (Bergem, Nilsen & Scherer, 2016) har mellom anna funne at det er lite bruk av oppgåver som er kognitivt utfordrande, rike oppgåver og problemløysingsoppgåver. Elevane tenkjer først på løysinga dei allereie hadde funne i den førre oppgåva, men dei finn ut at det finst fleire løysingar og held fram med å undersøkje det i lag.

Oppgåve 1c: Det er 4 myntar i posen. Kva for myntar og kor mange kroner kan det vere? Oppgåve 1a) spesifiserte både talet på myntar og summen, og oppgåve 1b) spesifiserte summen, men ikkje talet på myntar. I oppgåve 1c) vrir ein på det og spesifiserer talet på myntar, men ikkje kva for sum det skal vere. Til liks med 1b) er dette ei oppgåve med fleire, men endeleg mange løysingar innanfor konteksten med norske myntar. Fleire av elevgruppene tolka oppgåva slik at dei fire myntane måtte ha same verdi, og var difor tilfredse når dei fann svaret 1 + 1 + 1 + 1 = 4. Læraren måtte oppmuntre elevane til å finne fleire løysingar. Nokre grupper så at dei kunne bruke svaret frå 1a), 10 + 5 + 1 + 1, medan andre fann svar med fire 5-arar, fire 10-arar eller fire 20-kroner. Berre tre elevgrupper kom fram til andre svar. Ei gruppe fann 10 + 10 + 1 + 1 = 22 og 10 + 10 + 5 + 5 = 30, medan to grupper fann 10 + 5 + 5 + 1 = 21. Ei av elevgruppene som hadde funne fleire svar, byrja lure på om dei kunne bruke andre rekneoperasjonar enn addisjon.

376 Elev 1: Men det er ikkje mogeleg med fleire på fire.

378 Elev 2: Nei. Jo!

Dei held fram med å diskutere og skrive på arket sitt.

390 Elev 2: Sjå!

392 Elev 1: Det er jo 15

394 Elev 2: Ja, men minus

396 Elev 1: Hm … (ler) Eg trur ikkje vi har lov til det

Dei to elevane utforskar fleire reknestykke der dei brukar både pluss og minus. Dei har tydeleg fjerna seg noko frå konteksten med myntane og utforskar problemet med fire tal som rein matematikk. Dei er samstundes i tvil om dei er på rett veg.

408 Elev 1: Har vi lov til minus da?

410 Elev 2: Hm, har vi faktisk lov?

Dei finn ut at dei må spørje læraren om det er lov å bruke minus.

416 Elev 2: Er det lov med minus, for det er ikkje fleire tal?

I denne utforskingssekvensen utfordrar elevane valet av matematisk modell, som jo er den andre av dei tre måtane å vere kritisk på som Askew (2015) identifiserte. Det er ikkje innanfor modellen eller den gjevne konteksten å tenkje at ein kan subtrahere myntar. Desse elevane er i den tidlege fasen med å lære seg både addisjon og subtraksjon, så det er naturleg at dei utforskar om båe reknemåtane kan kome i spel, altså kva for matematisk operasjon som er gyldig i ein gjeven situasjon. Reint matematisk er jo subtraksjon en del av den additive konteksten.

Oppgåve 2a: Kari har 5 myntar i posen sin. Til saman er det 20 kr. Kva for myntar har Kari i posen sin? Denne oppgåva skil seg frå dei førre oppgåvene ved at den ikkje har noka løysing innanfor konteksten med norske myntar. I skulen er det ikkje vanleg å gje elevane oppgåver som ikkje kan løysast, så elevane gøyv laus på oppgåva i god tru.

468 Elev 1: OK, det blir enkelt. Nei, kva …

470 Elev 2: Fire myntar?

472 Elev 1: Nei. Ho har fem myntar oppi. I posen sin.

Dei to elevane held fram med å prøve ut ulike tal for å sjå kva som kan stemme. Elevane klarer ikkje å finne svar på oppgåva, men dei er vande med at oppgåver har løysing, så dei er ikkje viljuge til å gje opp.

511 Elev 1: Vi må ha ein …. Det går ikkje

513 Elev 2: Ja, men det må jo gå.

Elevane kjem etter ei stund fram til at det går an å løyse oppgåva dersom ein kan bruke andre myntar enn dei myntane dei har tilgjengelege:

527 Elev 1: Det går viss det hadde funnest ein toar.

(…) 

567 Elev 2: Fire. Viss vi treng berre, så … viss det skulle vore pluss 19, så skulle vi ha funne svaret no! Eller med ein einaste gong. Det skulle berre funnest toarmyntar.

Ikkje alle matematikkproblem har løysingar, og mange reknestykke kan ikkje løysast innanfor ei gjeve talmengd. Å tørre å utvide konteksten er difor ein viktig lærdom om kva kritisk tenking i matematikk kan vere, og som elevane er i ferd med å byggje opp når dei seier at oppgåve 2a), kan løysast dersom dei har 2-kronemyntar. Nokre av elevane som jobba med oppgåve 2a) blei kritiske til kvifor dei fekk ei oppgåve som ikkje har løysing.

445 Elev 3: Så dette er ei tulleoppgåve?

447 Lærar: Eller ei umogeleg oppgåve.

451 Elev 3: Lagde de ho slik at vi ikkje skulle få ho til, berre slite og slite?

Askew (2015) nemner «questioning the contexts and motives for what is being modelled» (s. 708) som døme på å vere kritisk til kva som blir modellert. Desse elevane utfordrar motivet for å gje dei oppgåver som ikkje har noko svar, noko dei tydeleg ikkje er vande med, og stiller spørsmål ved konteksten oppgåva er gjeven innanfor. Med andre ord er elevane kritiske til kva som blir modellert matematisk, som jo var det tredje aspektet ved å vere kritisk som Askew (2015) nemnde.

Diskusjon

I matematikk er det eit sentralt poeng at ei oppgåve kan ha ei eintydig, fleire, uendeleg mange eller inga løysing. Dette opplever elevar i for liten grad i skulematematikken, og gjerne ikkje før dei kjem til vidaregåande skule og skal løyse andregradslikningar. Eit viktig poeng er at å støyte på problem som det ikkje ser ut til å vere mogeleg å løyse, leier til ei utviding av domenet, talsystemet eller liknande slik at det likevel er mogeleg å finne ei løysing. Slik har ein til dømes historisk utvikla rasjonale tal frå heiltal, innsett at det finst irrasjonale tal, utvikla negative tal frå positive tal og komplekse tal frå reelle tal. I dag kan ein jo lett gje enkle rekneoppgåver som gjenskaper denne utvidinga av talmengdene, men ifølgje IBL-modellen er det betre å sette elevane i situasjonar der dei sjølve opplever behovet for å utfordre rammene. Det handlar både om å byggje opp ein klasseromskultur der mål og eigarskap til kunnskapen er felles, at å forstå matematikkens natur er eit ønskt utbytte, og at læringsmiljøet bør handle om at elevane utviklar evner til å forklare fenomen.

Når elevane seier at oppgåva med å bruke fem myntar til å sette saman 20 kroner ikkje kan løysast med dei norske myntane, men at det går an å finne ei løysing dersom dei hadde 2-kroningar, så er det eit døme på korleis ei oppgåve som ikkje har løysing innanfor ei gjeven ramme kan løysast om vi utvidar rammene. Innanfor matematikken finst det mange døme på dette. 3–5 har inga løysing innanfor mengda av naturlege tal, 3:5 har inga løysing innanfor heiltala, x² + 1 = 0 har ikkje løysing innanfor mengda av reelle tal. Ved å utvide frå naturlege tal til heiltal, frå heiltal til rasjonale tal og frå reelle tal til komplekse tal, kan alle desse problema løysast.

Å sjå løysingar som ikkje er mogelege innanfor dei rammene som er gjevne, slik som til dømes å sjå at ein kan få til å setje saman fem myntar til å bli 20 kroner dersom ein har 2-kroningar, er ein form for kritisk tenking i matematikk. Å tenkje kritisk i matematikk handlar òg om å prøve ut, sjå for seg, tenkje på andre vegar til målet, andre løysingar, andre algoritmar, og sjå for seg korleis ein kan få til noko ved å tenkje på ein annan måte enn den vanlege eller den som det er lagt opp til frå læraren.

Det er òg viktig at elevane får arbeide med oppgåver som har meir enn éi eintydig løysing, ikkje minst sidan matematikkfaget i for stor grad har blitt framstilt som eit fag med eintydige oppgåver med eintydige løysingsmåtar fram mot eintydige svar. Det er difor av stor nytte at ein allereie frå byrjinga av skuleløpet let elevane arbeide med oppgåver med fleire svar og som kan bli løyst på mange måtar.

Den mangefasetterte forståinga av IBL med kjenneteikn innan fem område vist i figur 1 blei brukt som guide under planlegginga av undervisninga. Analysen viser at ein kunne finne fleire av kjenneteikna i leksjonane. Læringsmiljøet blei prega av oppgåver som gav rom for ulike mogelege løysingsstrategiar, og sett bort frå oppgåve 1a) hadde alle oppgåvene fleire mogelege svar. Vidare kunne oppgåvene opplevast som verkelege for elevane, og det var tilgang til verktøy som leikemyntar, tal-liner, papir og blyantar. Elevane blei oppmuntra til å forklare løysingane sine, noko læraren la stor vekt på både i byrjinga av timen og medan elevane arbeidde i par. Dei realistiske avgrensingane på myntproblema ved å bruke berre norske myntar gav for det første elevane mogelegheiter til å oppdage at ikkje alle problema kan løysast med desse avgrensingane; for det andre at viss det fanst ein mynt med verdi 2 kroner, kunne problemet løysast; og for det tredje, at det i den verkelege verda faktisk ikkje finst nokon mynt i Noreg med verdi 2 kroner. Å forstå kva ei løysing tyder, under kva for omstende og avgrensingar løysingar kan bli funne, og å kunne sjå at endring av vilkåra kan føre til andre løysingar, er ein viktig del av å lære matematikk, og særleg ein viktig del av å utvikle ei kritisk orientering i matematikk, som t.d. identifisert av Goos et al. (2014) og Askew (2015). I tillegg er det òg ein viktig del av kva det vil seie å løyse problem i samfunnet. Dette leier oss nærare til dei aspekta ved å lære matematikk som blir foreslått av Frankenstein (2009) og Skovsmose (1998, 2008), og som er nokre av dei underliggjande ideane og ønskte resultata av IBL (Maaß & Reitz-Koncebovski, 2013).

For nokre elevar, som elevane 1 og 2, observerte vi at dei måtte oppfordrast til å skrive og teikne av læraren. Dei hadde allereie løyst problemet ved hjelp av leikemyntane, men ikkje skrive noko. Å lære å kommunisere løysinga og gjere tankane sine synleg for andre på ulike vis er ein viktig del av å utvikle matematisk literacy. Samstundes kan det å tvinge elevane til å representere svara sine på bestemde måtar verke distraherande for læringa av det matematiske innhaldet, og hindre dei frå å forfølgje det matematiske innhaldet djupare. Spaninga mellom på eine sida å styre elevane mot bestemde representasjonar og på hi sida la dei utforske fritt er noko vi må leve med. Ved å understreke tydinga av å skrive eller teikne som representasjonar og som middel for å formidle resultat risikerer ein å redusere tydinga av andre, til dømes munnleg kommunikasjon.

Frå empirien ser vi òg at elevane er involvert i utforskingssyklusen med dei fem E-ane, engasjere, explore (utforske), explain (forklare), extend (utvide) og evaluere medan dei arbeider saman i par. Læraren oppfordra elevane til å resonnere ved å spørje elevane om måtane deira å tenkje på, både i plenum og når elevane jobba parvis. Frå empirien er det tydeleg at læraren måtte understreke for elevane at dei skulle samarbeide og diskutere, sjølv om dette leidde til at når det blei gjort i plenum, blei det sett på som «forstyrrande» for nokre elevar, som det går fram av transkripsjonsline 24 ovanfor. Utvikling av ein klasseromkultur som verdset spørsmålsstilling, utforsking og kor feil blir sett på som ein nødvendig del av å lære matematikk, blir vektlagt som viktig i IBL (Maaß & Reitz-Koncebovski, 2013), og er viktig for at elevane skal utvikle ein kritisk disposisjon som er ein viktig komponent i matematisk literacy. I våre data er det tydeleg korleis læraren prøvde å oppnå dette, både gjennom hennar erfaring som lærar og ved å bruke ein IBL-orientert undervisningsplan.

Det er ikkje rett fram å svare på spørsmålet om kva det tyder å vere kritisk i ein matematikktime, særleg på lågare skulesteg. I ein liten studie som den vi har skrive om her, kan vi ikkje gjere krav på å ha generelle eller vidfemnande svar. Dataa våre viser døme på at det er mogeleg å identifisere dei tre måtane å vera kritisk på som Askew (2015) identifiserte, sjølv i 2. klasse. Vi har sett korleis dette er mogeleg gjennom at innstillinga og atmosfæren i klasserommet er oppmuntrande, ved at klasseromkulturen og læringsmiljøet er som beskrive i IBL-modellen. Eit nøkkelmoment her var at oppgåvene som elevane fekk, bar i seg potensial til fleire løysingar og ulike løysingsmetodar. Å planlegge undervisning ved hjelp av ein IBL-modell som den som blei brukt her, ser difor ut til å kunne bidra til å fremme matematisk literacy, inkludert ei kritisk haldning. Samstundes ser vi på undersøkinga vår berre som eit lite bidrag til ein større diskusjon om kva kritisk tenking i matematikk og matematikkundervisninga på dei låge klassetrinna kan vere.